asdar.id menyediakan Member Premium Download untuk download file tanpa embel-embel iklan dan halaman, apa lagi harus menunggu timer yang begitu lama. Dengan berlangganan Member Premium Download, semua file dapat didownload dengan singkat langsung menuju ke sumbernya!, klik DISINI untuk DAFTAR atau DISINI untuk LOGIN :-) Jika ada pertanyaan silahkan hubungi Admin DISINI. Untuk cara download file Member Free Download, bisa membaca Tutorial Download yang ada dibawah Timer (halaman Safelink) saat menekan tombol download.
asdar.id menyediakan Member Premium Download untuk download file tanpa embel-embel iklan dan halaman, apa lagi harus menunggu timer yang begitu lama. Dengan berlangganan Member Premium Download, semua file dapat didownload dengan singkat langsung menuju ke sumbernya!, klik DISINI untuk DAFTAR atau DISINI untuk LOGIN :-) Jika ada pertanyaan silahkan hubungi Admin DISINI. Untuk cara download file Member Free Download, bisa membaca Tutorial Download yang ada dibawah Timer (halaman Safelink) saat menekan tombol download.
Mungkin ada beberapa teman-teman proyek tidak mengetahui rumus tinggi balok beton bertulang itu apa. Misal, ukuran lantainya (3,2 m x 4,8 m). Untuk yang bentang 4,8 meter, ukuran baloknya 20/30 cm. Apakah aman atau tidak? Disini penulis tidak berani menjawab jawab aman atau tidak. Untuk perencanaan struktur tidak semudah itu.
Banyak faktor yang harus ditinjau untuk menyatakan suatu elemen struktur dalam hal ini balok aman atau tidak. Tiap-tiap bangunan itu unik. Tidaklah sama antara bangunan yang satu dengan yang lainnya.
Meskipun kadang bangunan tersebut bangunan yang tipikal dan berada di lokasi yang sama, kata salah seorang Dosen UGM.
Rumus Tinggi Balok Beton Bertulang
Kembali lagi ke topik di atas. Bagaimanakah menentukan tinggi balok beton bertulang? Rumus tinggi balok beton Bertulang apa? Bagaimana cara menghitungnya?
Sebelum kita bahas, terlebih dahulu kita lihat dulu apa definisi balok itu.
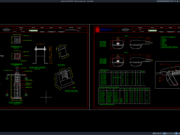
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut.
Sedangkan balok beton bertulang adalah elemen dari sebuah bangunan struktur beton bertulang yang berbentuk persegi, dengan posisi letak horizontal/diagonal, mendukung lantai atau tidak dan lebih dominan menerima bending ketimbang gaya aksial.
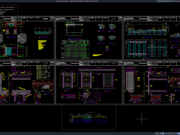
Kalau kita mengikuti pedoman yang ada pada SNI 2847_2013 tentang Persyaratan Beton Struktural Untuk Bangunan Gedung (download disini), maka Rumus Tinggi Balok Beton Bertulang adalah sebagai berikut:
Untuk menjawab pertanyaan di atas, maka tinggi balok beton bertulang untuk bentang 4,8 meter adalah 4800/21 (asumsi kedua ujung balok menerus), diperoleh 228 ~ ambil 300 mm.
Maka tinggi balok 20/30 Aman (Catatan: Aman dalam hal tinggi, faktor lain belum ditinjau).
Namun, kita masih sering menjumpai kebanyakan structural engineer mengambil patokan rumus tinggi balok beton bertulang 1/12 ~ 1/15 bentang (L). Bahkan penulis-pun sering menggunakan rumus ini dalam menentukan tinggi balok. Apakah Anda juga sama?
Dari mana angka 1/12 ~ 1/15 L diperoleh? Jika kita perhatikan tabel di atas, disitu tertulis bahwa rumus tersebut adalah untuk menentukan tinggi balok minimum. Artinya, kita boleh menggunakan tinggi balok lebih dari itu.
Jika Anda tahu persis dari mana angka 1/12 ~ 1/15 L diperoleh, silahkan tulis di kolom komentar agar kita sama-sama mengetahui dasarnya.
Sumber referensi: blog.nobelconsultant.com
Sekian postingan kali ini, semoga bermanfaat untuk rekan-rekan semua. Jangan lupa share artikel ini ke sosial media agar yang lain bisa mendapatkan ilmunya juga.