Setelah sebelumnya kita membahas mengenai Rumus Tinggi Balok Beton Bertulang, dimana pada bahasan tersebut terdapat empat kategori balok yaitu tertumpu sederhana, satu ujung menerus, dua ujung menerus dan balok kantilever.
Kali ini penulis akan mencoba menggali sedikit mengenai kategori balok yang ke empat yaitu balok kantilever non prategang (selanjutnya kita sebut balok kantilever).
Batasan pembahasan kali ini adalah balok kantilever pada bangunan kecil seperti ruko dan rumah tinggal. Jadi bisa Anda bayangkan pembahasan ini akan sangat ringan.
Berapa tinggi balok kantilever minimum?
Pada tabel 9.5(a) SNI 2847-2013 disebutkan bahwa tebal (tinggi) minimum balok kantilever bila lendutan tidak dihitung adalah l/8. Dimana l adalah bentang balok.
Bentang balok kantilever dihitung dari muka kolom/ jepitan sampai ujung balok. Maka jika bentang balok kantilever adalah 3 meter maka tingginya adalah 3000/8 = 375 mm.
Berarti boleh kalau tinggi balok kantilever < l/8?
Kalau pernyataan pada SNI demikian, artinya boleh. Tapi lendutannya dihitung. Daripada merepotkan diri sendiri, mending ikut peraturan saja. Kecuali jika terpaksa, misal Arsitek minta balok tidak boleh tinggi.
Contoh kasus penggunaan rumus yang kurang tepat
Pada bangunan kecil sangat jarang kita temukan panjang balok kantilever sampai 3 meter. Selain karena tidak efektif, juga ada persyaratan lainnya yang harus dipenuhi.
Misal, kita menterjemahkan secara mentah-mentah rumus di atas, lalu ada bentang balok kantilever 5 meter (contoh ekstrim), kita main hajar saja. Maka di dapat tinggi balok 625 mm. Apakah itu salah? tidak juga.
Tapi kita lihat konsekuensinya, berapa bentang balok yang menahan beban kantilever tersebut. Berapa dimensi kolom yang menahan balok kantilever tersebut. Jangan-jangan baloknya memang kuat, tapi bangunannya jadi terguling.
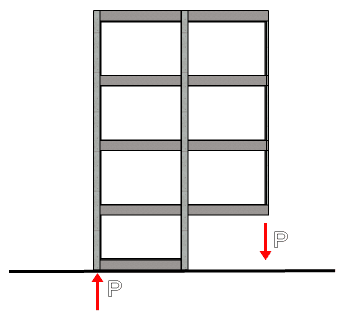Lebih-lebih lagi pada balok kantilever akan bekerja pada beban gempa vertikal. Apakah tidak bahaya? Bisa sih bisa, tapi kembali lagi ke konsekuensinya.
Tentu pada gambar diatas tidak bisa pakai pondasi telapak (footplate), karena pada kolom dibelakangnya beban sudah melawan gravitasi. Setidaknya dibutuhkan pondasi tiang pancang yang tahan cabut. Kalau dirunut-runut lagi, ujung-ujungnya jatuh ke cost/biaya.
Sedangkan jelas tujuan kita mendesain struktur guna mendapatkan bangunan yang kuat dan ekonomis. Disinilah Engineering Judgement diperlukan.
Jika memang tidak terpaksa sekali maka sebaiknya jangan membuat kantilever yang panjang seperti itu, akan ada banyak konsekuensinya. Mungkin balok kantilever konvensional sudah tidak sanggup juga dan harus pakai balok prestress.
Salah satu cara menentukan tinggi balok kantilever
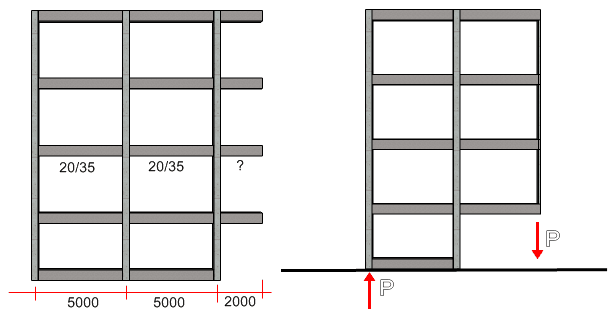
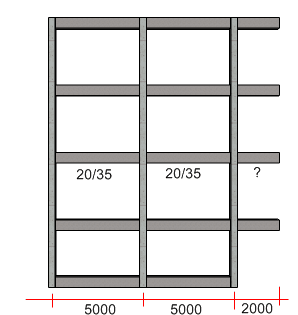Pada contoh gambar di atas. Jika kita menggunakan rumus l/8 maka diperoleh tinggi balok 25 cm.
Akan tetapi jika disuruh memilih, penulis akan mendesainkan dengan tinggi 35 cm. Artinya sama dengan tinggi balok dibelakangnya. Mengapa?
Alasannya adalah dari segi pelaksanaan menjadi lebih mudah untuk meneruskan tulangan balok dibelakangnya dan membuat bekistingnya. Jadi apakah akan boros beton?
Ya tentu, tapi dengan menambah tinggi baloknya yang tidak signifikan, maka jumlah tulangannya jadi lebih hemat. Silahkan pilih, ini adalah opsional.
Untuk lebih memperjelas pemahaman kita mengenai balok kantilever, ada baiknya kita bahas contoh soal mendesain tulangan balok kantilever sebagai berikut:
Contoh 1
Properti material
- fc’ (mutu beton) = 30 MPa
- fy (mutu baja) = 390 MPa
- ß = 0.85
Dimensi profil balok kantilever
- Lebar balok = 300 mm
- Tinggi balok = 400 mm
- Cover = 30 mm
- Maka, tinggi balok efektif = 400 – 30 = 370 mm
Pembebanan
- Momen maksimum, Mu = 100 kNm
- Momen nominal, Mn = Mu/θ(0.8)
Desain tulangan lentur
- Rn = Mn/bd^2 = 3,04
- m = fy/0.85 fc = 15.29
- ρ = 1/m (1-(1-2Rnm/fy)^0.5)) = 0.00834
- ρ min = 1.4/fy = 0.00359
- ρ max = 0.75*((0.85*fc*β)/fy)*(600/(600+fy)) = 0.02526
- Karena ρ min > ρ > ρ max, maka As = ρbd = 925.23 mm^2
- Gunakan tulangan diameter 16 mm maka, n = As / ( π / 4 * D^2 ) = 4.60 ~ 5 Batang
Contoh 2
Dimana kita hanya merubah tinggi balok tersebut pada contoh 1 dari 400 mm menjadi 600 mm.
Maka diperoleh;
- Rn = Mn/bd^2 = 1,28
- m = fy/0.85 fc = 15.29
- ρ = 1/m (1-(1-2Rnm/fy)^0.5)) = 0.00338
- ρ min = 1.4/fy = 0.00359
- ρ max = 0.75*((0.85*fc*β)/fy)*(600/(600+fy)) = 0.02526
- Karena ρ min > ρ, maka As = ρmin bd = 613.85 mm^2
- Gunakan tulangan diameter 16 mm maka, n = As / ( π / 4 * D^2 ) = 3.05 ~ 3 Batang
Kesimpulannnya:
- Rumus digunakan sebagai pedoman awal dalam penentuan dimensinya.
- Lebih baik boros di beton sedikit tapi hemat banyak di tulangan.
- Meninjau balok kantilever sebaiknya melihat bangunan secara keseluruhan.
- Rumus adalah dasarnya, engineering judgement adalah penentunya.
Artikel ini dibuat berdasarkan pengalaman penulis dalam mendesain struktur bangunan. Mohon saran jika terdapat kesalahan dan kekeliruan dalam artikel ini.
Sumber referensi: blog.nobelconsultant.com
Sekian artikel kali ini, semoga bisa bermanfaat untuk kita semua. Jangan lupa share artikel ini ke sosial media agar yang lain bisa membacanya juga. Sampai jumpa pada artikel berikutnya.
