asdar.id menyediakan Member Premium Download untuk download file tanpa embel-embel iklan dan halaman, apa lagi harus menunggu timer yang begitu lama. Dengan berlangganan Member Premium Download, semua file dapat didownload dengan singkat langsung menuju ke sumbernya!, klik DISINI untuk DAFTAR atau DISINI untuk LOGIN :-) Jika ada pertanyaan silahkan hubungi Admin DISINI. Untuk cara download file Member Free Download, bisa membaca Tutorial Download yang ada dibawah Timer (halaman Safelink) saat menekan tombol download.
Metode polygon adalah salah satu cara penentuan posisi horizontal banyak titik dimana titik satu dengan yang lainnya dihubungkan satu sama lain dengan pengukuran sudut dan jarak sehingga membentuk rangkaian titik-titik (polygon). Untuk lebih jelasnya silahkan baca Teknik Pengukuran Luas Tanah Menggunakan Theodolite dengan Metode Polygon Tertutup.
Pengukuran dan pemetaan polygon merupakan salah satu metode pengukuran dan pemetaan. Kerangka dasar horizontal yang bertujuan untuk memperoleh koordinat planimetris (x,y) titik-titik pengukuran.
Pengukuran Kerangka Dasar Horisontal (KDH):
- Metode titik tunggal
- Pengikatan kemuka
- Pengikatan kebelakang
Pengikatan kebelakang di bagi dua metode:
- Metode collins
- Metode cassini
- Metode titik banyak
Banyak titik di bagi lima metode:
- Metode polygon
- Metode triangulasi
- Metode trilaterasi
- Metode triangulterasi
- Metode kuadrilateral
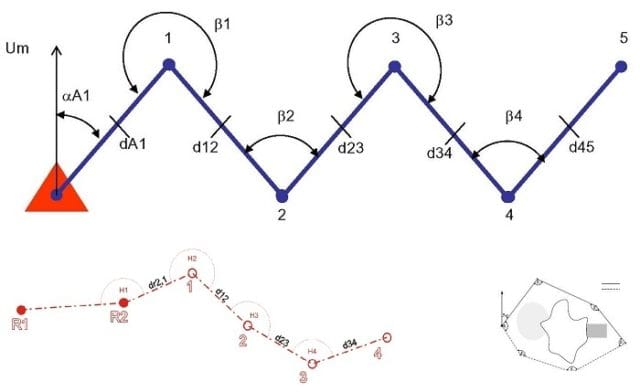
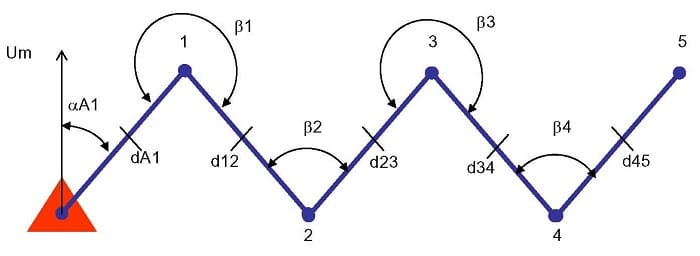
Pengukuran polygon sendiri mengandung arti salah satu metode penentuan titik diantara beberapa metode penentuan titik yang lain. Berdasarkan bentuknya polygon dapat dibagi dalam dua bagian, diantaranya:
Polygon berdasarkan visualnya
Polygon berdasarkan visualnya, macamnya adalah:
a. Polygon tertutup
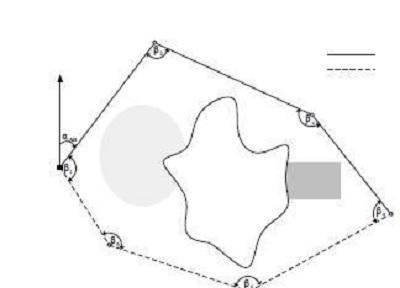
Pada polygon tertutup:
- Garis-garis kembali ke titik awal, jadi membentuk segi banyak.
- Berakhir di stasiun lain yang mempunyai ketelitian letak sama atau lebih besar daripada ketelitian letak titik awal.
- Polygon tertutup memberikan pengecekan pada sudut-sudut dan jarak tertentu, suatu pertimbangan yang sangat penting.
- Titik sudut yang pertama = titik sudut yang terakhir.
Polygon tertutup biasanya dipergunakan untuk:
- Pengukuran titik kontur.
- Bangunan sipil terpusat.
- Waduk.
- Bendungan.
- Kampus UPI.
- Pemukiman.
- Jembatan (karena diisolir dari 1 tempat).
- Kepemilikan tanah.
- Topografi kerangka.
b. Polygon terbuka
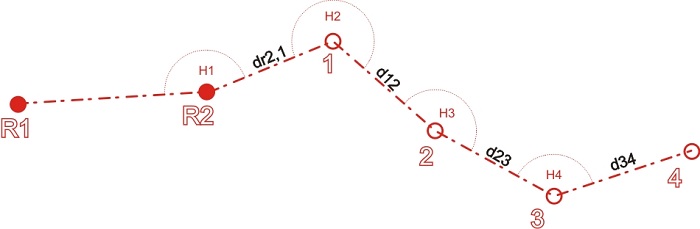
Polygon terbuka (secara geometris dan matematis) terdiri atas serangkaian garis yang berhubungan tetapi tidak kembali ke titik awal atau terikat pada sebuah titik dengan ketelitian sama atau lebih tinggi ordenya. Titik pertama tidak sama dengan titik terakhir.
Polygon terbuka biasanya digunakan untuk:
- Jalur lintas / jalan raya.
- Saluran irigasi.
- Kabel listrik tegangan tinggi.
- Kabel TELKOM.
- Jalan kereta api.
c. Polygon bercabang
Dilihat dari geometris, polygon terbagi menjadi 3, yaitu:
1. Polygon terikat sempurna
Dikatakan polygon terikat sempurna, apabila:
- Sudut awal dan sudut akhir diketahui besarnya sehingga terjadi hubungan antara sudut awal dengan sudut akhir.
- Adanya absis dan ordinat titik awal atau akhir.
- Koordinat awal dan koordinat akhir diketahui.
2. Polygon terikat sebagian
Dikatakan polygon terikat sebagian, apabila:
- Hanya diikat oleh koordinat saja atau sudut saja.
- Terikat sudut dengan koordinat akhir tidak diketahui.
3. Polygon tidak terikat
Dikatakan polygon tidak terikat, apabila:
- Hanya ada titik awal, azimuth awal, dan jarak. Sedangkan tidak diketahui koordinatnya.
- Tidak terikat koordinat dan tidak terikat sudut.
Dilihat dari geometris, polygon terbagi menjadi 3, yaitu:
- Polygon terikat sempurna
- Polygon terikat sebagian
- Polygon tidak terikat
Untuk mendapatkan nilai sudut-sudut dalam atau sudut-sudut luar serta jarak-jarak mendatar antara titik-titik polygon diperoleh atau diukur dari lapangan menggunakan alat pengukur sudut dan pengukur jarak yang mempunyai tingkat ketelitian tinggi.
Pengolahan data polygon dikontrol terhadap sudut-sudut dalam atau luar polygon dan dikontrol terhadap koordinat baik absis maupun ordinat. Pengolahan data polygon dimulai dengan menghitung sudut awal dan sudut akhir dari titik-titik ikat polygon.
Kontrol sudut polygon diawali terlebih dahulu dilakukan yaitu untuk memperoleh koreksi sudut polygon dengan cara mengontrol jumlah sudut polygon terhadap pengurangan sudut akhir dengan sudut awal polygon. Koreksi sudut polygon yang diperoleh kemudian dibagi secara merata tanpa bobot terhadap sudut-sudut polygon hasil pengukuran dan pengamatan di lapangan.
Sudut-sudut jurusan titik polygon terhadap titik polygon berikutnya mengacu terhadap sudut awal polygon dijumlahkan terhadap sudut polygon yang dikoreksi. Kontrol Koordinat berbeda dengan kontrol sudut yaitu koordinat akhir dan awal dikurangi serta dibandingkan terhadap jumlah proyeksinya terhadap absis dan ordinat.
Koreksi absis dan ordinat akan diperoleh dan dibandingkan dengan mempertimbangkan bobot kepada masing-masing titik polygon. Bobot koreksi didekati dengan cara perbandingan jarak pada suatu ruas garis terhadap jarak total polygon dari awal sampai dengan akhir pengukuran.
Syarat Geometris
Jenis-jenis Polygon
Berdasarkan bentuknya polygon dibagi dalam dua bagian, diantaranya:
Jenis Polygon secara Visual:
A. Polygon Tertutup
Polygon tertutup adalah polygon yang bermula dan berakhir pada satu titik yang sama. Polygon tertutup sering disebut polygon kring (kring polygon). Ditinjau dari segi pengkatannya (azimut dan koordinat), terdapat beberapa variasi seperti:
- Tanpa ikatan
- Terikat hanya azimut
- Terikat hanya koordinat
- Terikat azimut dan koordinat
Keuntungan dari polygon tertutup yaitu, walaupun tidak ada ikatan sama sekali, namun koreksi sudut dapat dicari dengan adanya sifat polygon tertutup yang jumlah sudut dalamnya sama dengan (n-2) 1000. Selain itu, terdapat pula koreksi koordinat dengan adanya konsekuensi logis dari bentuk geometrisnya bahwa jumlah selisih absis dan jumlah selisih ordinat sama dengan nol.
Keuntungan inilah yang menyebabkan orang senang dengan bentuk polygon tertutup. Satu-satunya kelemahan polygon tertutup yang sangat menonjol adalah bahwa bila ada kesalahan yang proporsional dengan jarak (salah satu salah sistematis) tidak akan ketahuan, dengan kata lain walaupun ada kesalahan tersebut, namun polygon tertutup itu kelihatan baik juga. Jarak-jarak yang diukur secara elektronis sangat mudah dihinggapi kesalahan seperti itu, yaitu kalau ada kesalahan frekuensi gelombang.
Kelemahan polygon tertutup yaitu, bila ada kesalahan yang proporsional dengan jarak (salah satu salah sistematis) tidak akan ketahuan. Dengan kata lain, walaupun ada kesalahan, namun polygon tertutup kelihatan baik juga. Jarak-jarak yang diukur secara elektronis sangat mudah dihinggapi kesalahan seperti kesalahan frekuensi gelombang.
Pada Polygon Tertutup:
- Garis-garis kembali ke titik awal, jadi membentuk segi banyak.
Berakhir di stasiun lain yang mempunyai ketelitian letak sama atau lebih besar daripada ketelitian letak titik awal.
B. Polygon Terbuka
Yang dimaksud dengan polygon terbuka adalah polygon yang titik awal dan titik akhirnya merupakan titik yang berlainan (bukan satu titik yang sama). Polygon terbuka ini dapat kita bagi lebih lanjut berdasarkan peningkatan pada titik-titik (kedua titik ujungnya). Ada dua macam peningkatan untuk polygon terbuka ini yaitu:
- Peningkatan azimut
- Peningkatan koordinat
Berdasarkan peningkatan-peningkatan itu, maka polygon terbuka dapat dibagi lebih lanjut menjadi:
- Tanpa ikatan sama sekali.
- Pada salah satu ujung yang lain tanpa ikatan sama sekali.
- Pada salah satu ujungnya terikat azimut saja, sedangkan pada ujung yang lain tanpa ikatan sama sekali.
- Pada salah satu ujungnya terikat azimut dan koordinat, sedangkan pada ujung yang lain tanpa ikatan sama sekali.
- Pada kedua ujungnya masing-masing terikat azimuth.
- Pada salah satu ujungnya terikat koordinat, sedangkan ujung yang lain terikat azimuth.
- Pada kedua ujungnya masing-masing terikat koordinat.
- Pada salah satu ujungnya terikat azimut dan koordinat, sedangkan ujung yang lain terikat azimut saja.
- Pada salah satu ujungnya terikat azimut dan koordinat, sedangkan ujung yang lain terikat koordinat.
- Pada kedua ujungnya masing-masing terikat baik azimut maupun koordinat.
- Pada kedua ujungnya masing-masing terikat baik azimut maupun koordinat.
Penulis: agus saputra dari http://tekniksipilinfo.blogspot.com
Sekian postingan kali ini mengenai Definisi, Syarat, dan Macam Pemetaan dengan Metode Polygon, semoga bisa menambah wawasan kita semua. Jangan lupa share artikel ini ke sosial media agar yang lain bisa mendapat manfaatnya.
